Some of the most popular public essential cryptography standards like RSA, DSA, and DH that are in use these days can be broken in a quantum computer. However, the vital point to note is that in case if practical QCs turns out to reality, there is always the possibility that they might pose a risk to PKI-based signatures. Just, for example, someone with a QC could perform a man-in-the-middle attack for a captured TLS negotiation. Signatures are often utilized and help in ensuring that the software is genuine and from an identified entity. In another situation, if a signature is made used to confirm the integrity of software, then it is burned into a piece of hardware. A QC at times could falsify a signature and cope to load an arbitrary else spiteful image. Hence, it is because of these reasons, at most of the leading companies, management has started to invest quantum-secure hash-based signatures.
Today we can relate a quantum-secure signature technique more equivalent to Hash-Based Signatures (HBS). Usually, hash-based signatures are more like tree structures that feature signatures of messages more like their leaves, and the path to the source of the tree could be well considered as the public key for the words signed in the tree. It is because of its well-understood and studied primitives, Hash-Based Signatures schemes are now broadly acknowledged as the most effective and good candidates for quantum-secure signatures.
Nowadays, various problems that many of us are witnessing on the Internet are related to the lack of trust while performing different transactions. Just, for example, daily emails that one receives, or websites that any of us visit very often have got little trust built into them. Consequently, there has been a steep rise in the creation of digital signatures and signing our messages with a private key.
Public vital strategies give us methods for both validating the sender, and the respectability of the technique. Shockingly the vast majority of the strategies which are utilized to make these marks, for example, with prime number factorization (likewise with RSA) and in elliptic bend techniques, will be broken with quantum PCs.
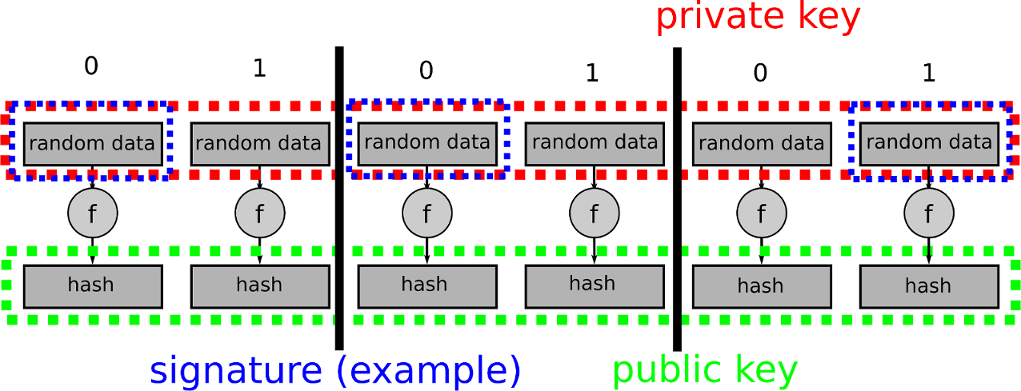
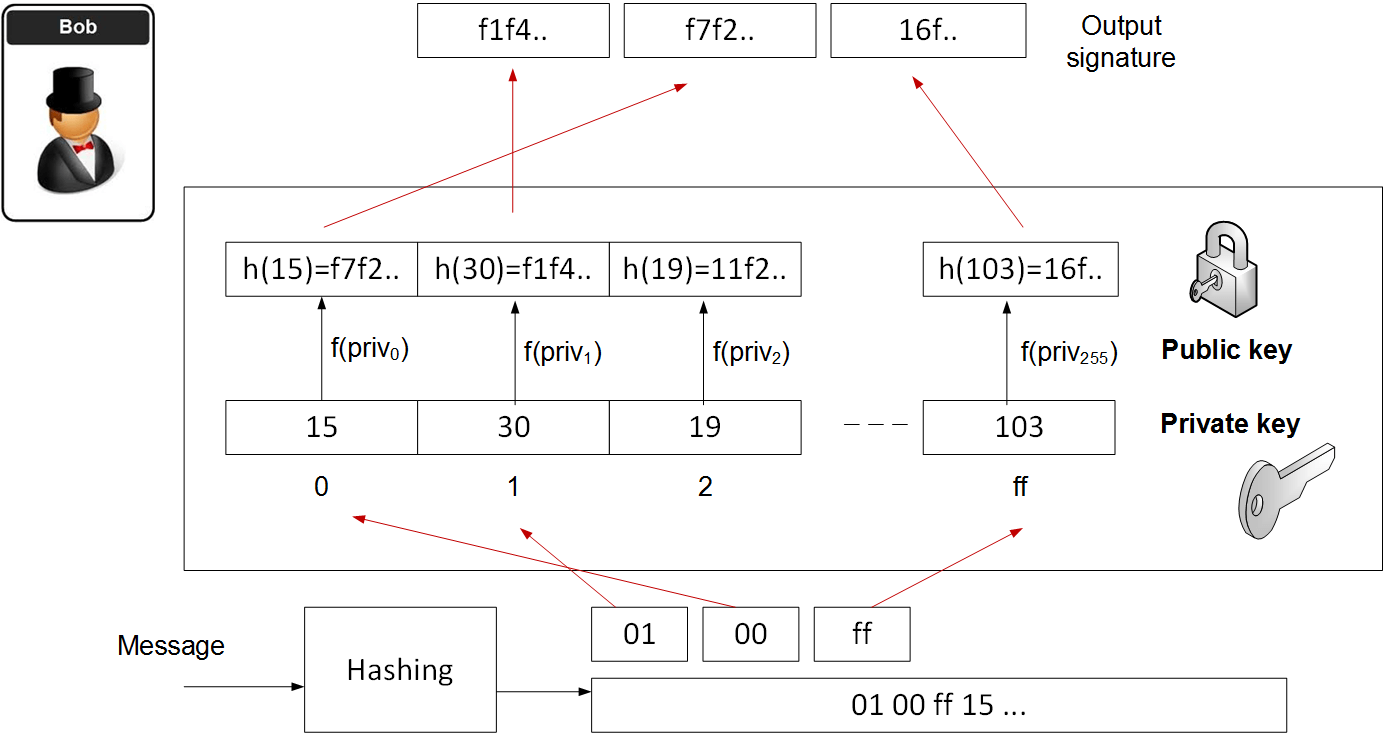
Hash to obtain Random Subset (HORS) is a quantum powerful hashed-based one-time signature. With this, we make a progression of whole numbers for our private keys and sort out into an indexable frame. At that point, we hash them to an arrangement of public key qualities. Next, we fragment the hash of the message into a progression of n-bit whole number qualities. The mark is then accomplished through a gaze upward of the incentive in the general population key rundown.

Let us assume that you need to segment the hash into 8-bit values and for a 128-bit hash (using MD5), the method is then:
- Create 256 random values. These are our private key values (priv0… priv255).
- Hash each of the private key values to produce a list of our public key values pub. These will be indexed.
- Hash the message (M) for a 128-bit hash (h), and which will produce 16 8-bit values (hi).
- Take each of the values (hi) and use as a lookup to the public key value.
Now, if you are a Stefen or Bob, and creates the public key and the private key, then it directly means that you are also building the message, and then adds the hash-based signatures. Moreover, you show Alice the message and the message, and the public key. As a Stefen or Bob, you are showing that you have the associated private key for this public. You just cannot use this key pair again, so will produce a new key pair for the next signature.
The following illustrates a simple example:
Background: Quantum Robust Hash-based signature schemes and functions
To understand hash-based signatures, it also gets essential to have some familiarity with cryptographic hash functions. Kindly note that these functions take some input string (naturally or a random length) and produce a fixed-size “digest” as output. Common cryptographic hash functions such as SHA2, SHA3 or Blake2 produce digests ranging from 256 bits to 512 bits.
For a function H(\cdot) to be considered a ‘cryptographic’ hash, it must reach some precise security necessities. There are a number of these, however, let us focus on three and the most frequently used ones:
1. Pre-image resistance (sometimes known as “one-wayness”): given some output Y = H(X), it should be time-consuming to find an input X such that H(X) = Y. (There are numerous caveats to this, but idyllically, the best such attack would require a time comparable to a brute-force search of whatever distribution X is drawn from.)
2. Second-preimage resistance: This is subtly different than pre-image resistance. Given some input X, it should be hard for an attacker to find a different input X’ such that H(X) = H(X’).
3. Collision resistance: It is never that easy to find any two values X_1, X_2 such that H(X_1) = H(X_2). Note that this is a much stronger assumption than second-preimage resistance, since the attacker has complete freedom to find any two messages of its choice.
The model hash capacities are accepted to give these properties. That is, no one has articulated a meaningful (or even conceptual) attack that breaks any of them. That could merely change, apparently, in which case we’d in all likelihood quit utilizing them.
Since we will likely utilize hash functions to develop signature conspires, it’s additionally useful to quickly review that primitive. An advanced signature plate is a public critical primitive in which a client (or “underwriter”) produces a couple of keys, called the general population key and private key. The client holds the private key and can utilize this to “sign” self-assertive messages — producing a resulting digital signature. Any individual who has ownership of general society key can check the rightness of a message and its related signature.
From a security point of view, the fundamental property, we need from a signature conspire is unforgeability, or “existential unforgeability.” This necessarily implies that an assailant (somebody who does not have the private key) ought not to have the capacity to fashion a strong signature on a message that you didn’t sign. For additional on the precise meanings of signature security.

